The two thirds of the average game is a great way of introducing game theory to students.
I've used this game on outreach events with +Paul Harper, at conferences with +Louise Orpin (when describing my outreach activities with other academics) and also in my classroom. I've blogged about the results before:
- School kids
- Postgraduate students
- OR 54 conference delegates
- MSc students (Note that one point of this post is to show better graphs than the ones on those posts)
The definition of the game from the wiki page is given here:
"In game theory, Guess 2/3 of the average is a game where several people guess what 2/3 of the average of their guesses will be, and where the numbers are restricted to the real numbers between 0 and 100, inclusive. The winner is the one closest to the 2/3 average."
I run this game once without any instruction. I just explain the rules and let them fill in the form in front of them (contained in this repo).
I then bring up slides discussing how iterated elimination of weakly dominated strategies leaves the "rational" strategy to be that everyone guesses 0.
After this I invite the participants to have a second guess. In general the results are pretty cool as you see the initial shift towards equilibrium. The fact that the winning guess in the second play of the game is in fact not 0 gives an opportunity to discuss irrational behaviour and also what would happen if we played again (and again...).
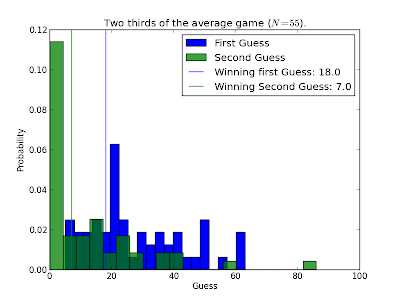
I've run this game a couple of times now and here's the graph of the histogram showing the results for all guesses I've recorded.
You certainly see that the guesses move after rationalising the strategies. Funnily enough though no one has guessed 100 during the first guess but a couple of people have in the second guess. I assume this is either some students trying to tell me that I'm boring them, trying to help a colleague win or I'm perhaps not doing a great job of explaining things :)
Here's some graphs from the individual events that I've collected data for:
- A talk I gave during a high school revision week:
- An outreach event with the MSI:
- MSc students from the 2012-2013 cohort:
- Academics at a talk on outreach at OR54 (the OR society annual conference):
- The OR society student conference SCOR2012:
- Academic at a talk on outreach at YOR18 (The OR society conference for early career academics):
Despite the low number of participants in some of the events they all show a a similar expected trend: the second guesses are lower. Surprisingly on one occasion the second winning guess was actually 1! This is a very quick move towards the theoretical equilibrium.
These experiments have been done on a much wider scale and in a much more rigorous way than my humble "bits of fun" for example the coursera game theory MOOC collect a bunch of data on this game and there's also a pretty big experiment mentioned in this talk:
Having said that I can't recall if other experiments look at successive guesses following an explanation of rational behaviour...
Github repo
I've put all the code used to analyse a game on github. It's a simple python file that can be pointed at a directory or a file and will produce the graph (using matplotlib) as well as spit out some other information. The data set for all these events (the first graph on this post) is also on there and if anyone would like to add to it please let me know :)
(There's also the handout that I use to get the student answers in the repo)
(If you found your way here because of interests in game theory this previous post of mine listing free OSS software for game theory might be of interest)
(If you found your way here because of interests in game theory this previous post of mine listing free OSS software for game theory might be of interest)






No comments:
Post a Comment